



Next: A meghatározása
Up: Az extremális Frobenius-probléma
Previous: Néhány becslés -ra
Tartalomjegyzék
A becslések után ismerkedjünk meg az extremális Frobenius prob-lémakör
eddigi eredményeivel. Ezeket részben az előző fejezetben is ismertettük.
Ott az oktatási vonatkozások hangsúlyozása, itt az eddigi eredmények
teljesebb megismertetése a célunk. A  -vel kapcsolatban több fontos
részeredmény is ismert.
-vel kapcsolatban több fontos
részeredmény is ismert.
Első lépésnek tekinthetjük két japán szerző, NAGATA és
MATSUMURA [21] 1961-ben megfogalmazott tételét:
TÉTEL 3.2.1
Legyenek  és
és  pozitív egészek,
pozitív egészek,
 Ekkor
Ekkor
Erre az öszefüggésre több eltérő bizonyítás is adható, amelyek közül egyre
utaltunk a 2. fejezetben.
Ezt az eredményt felhasználva ERDŐS 1971-ben folyóiratban kitűzött
problémaként jelentette meg a  -re és a
-re és a
 -re vonatkozó
tételt [5]. A kitűzött feladatra később az általa adott megoldást ismertették.
-re vonatkozó
tételt [5]. A kitűzött feladatra később az általa adott megoldást ismertették.
TÉTEL 3.2.2
Ha  pozitív egész, akkor
pozitív egész, akkor
Az ötletes kombinatorikus bizonyítást GRAHAMmel közösen kiterjesztették és 1972-ben
megszületett az az általánosabb tétel, amelyet közel húsz évig nem sikerült
egyetlen matematikusnak sem tovább javítania [6].
TÉTEL 3.2.3
Ha  és
és  pozitív egészek,
pozitív egészek,
 akkor
akkor
Lényegében ezzel párhuzamosan kis  -ekre is többen vizsgálták nemcsak
-ekre is többen vizsgálták nemcsak
 -t, hanem a minél pontosabb felső becslések keresésével közvetve
-t, hanem a minél pontosabb felső becslések keresésével közvetve
 -t is. A
-t is. A  kiszámítása alapján szinte nyilvánvaló, hogy
Az
kiszámítása alapján szinte nyilvánvaló, hogy
Az  esetet LEWIN [20] tisztázta szintén az 1970-es évek elején:
esetet LEWIN [20] tisztázta szintén az 1970-es évek elején:
Mind LEWIN, mind ERDŐS és GRAHAM
bizonyításaiban azzal válik teljessé a
 meghatározása, hogy megadnak olyan konkrét
meghatározása, hogy megadnak olyan konkrét  -ket, amelyekre
Ezek a konstrukciók mindegyik esetben vagy szomszédos számokból, vagy
két azonos differenciájú számtani sorozat egyesítéséből épülnek fel.
-ket, amelyekre
Ezek a konstrukciók mindegyik esetben vagy szomszédos számokból, vagy
két azonos differenciájú számtani sorozat egyesítéséből épülnek fel.
Ezután több mint másfél évtizedig, a menet közben egyre jobban kiterjedő
Frobenius problémakörnek ebben a szegmensében nem történt semmiféle
előrelépés. A következő áttörés DIXMIER 1990-ben megjelent [4] cikke
nyomán indult el és napjainkig is tart. DIXMIER francia matematikus
csoportelméleti interpretációval és a Kneser-tételt is felhasználva,
a fentebb említett 3.1.3. Tétel becslését élesítve nagyon pontos felső becslést
adott  -re.
-re.
DIXMIER ezzel bizonyította ERDŐS és GRAHAM
[7] egy 1980-ban publikált sejtését, mely szerint
A 3.2.5. Tétel becslése több fontos esetben a lehető legjobbnak bizonyult,
azaz megadható olyan
 halmaz, amelyre
halmaz, amelyre
 megegyezik (3.2.1) jobb oldalával. Ezeket az eseteket DIXMIER két tételben
rögzítette.
megegyezik (3.2.1) jobb oldalával. Ezeket az eseteket DIXMIER két tételben
rögzítette.
TÉTEL 3.2.7
Ha 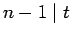 vagy
vagy
 , akkor
, akkor
TÉTEL 3.2.8
Amennyiben
 úgy
úgy
Amikor az  a
a  -nek osztója, a maximális értéket a
legnagyobb szomszédos címletek választásával érhetjük el. A másik két esetben
esetben
-nek osztója, a maximális értéket a
legnagyobb szomszédos címletek választásával érhetjük el. A másik két esetben
esetben
 differenciájú számtani sorozat lesz
a konstrukció alapja. Ezek a tételek azonnal adják az
differenciájú számtani sorozat lesz
a konstrukció alapja. Ezek a tételek azonnal adják az  -ra és az
-ra és az
 -re vonatkozó explicit formulákat. Ezekre DIXMIER
csak utal publikációjában [4].
-re vonatkozó explicit formulákat. Ezekre DIXMIER
csak utal publikációjában [4].
Legyen először  Ekkor két esetet vizsgálunk aszerint, hogy
a
Ekkor két esetet vizsgálunk aszerint, hogy
a  páros vagy páratlan. A páros esetben a 3.2.7. Tétel alapján
páros vagy páratlan. A páros esetben a 3.2.7. Tétel alapján
Amennyiben a  páratlan, tekintsük a 3.2.8. Tételt. Itt
páratlan, tekintsük a 3.2.8. Tételt. Itt  páros, így
Ez pontosan megegyezik a LEWIN-féle 3.2.4.Tétellel.
páros, így
Ez pontosan megegyezik a LEWIN-féle 3.2.4.Tétellel.
Hasonlóan kaphatjuk meg a pontos formulát az  esetben is.
Legyen először
esetben is.
Legyen először  , vagy
, vagy  . Alkalmazhatjuk a 3.2.7. Tételt,
és kapjuk, hogy
. Alkalmazhatjuk a 3.2.7. Tételt,
és kapjuk, hogy
Legyen most  ekkor
A két képlet az oszthatósági viszonyok ismeretében egységes alakban
is felírható:
ekkor
A két képlet az oszthatósági viszonyok ismeretében egységes alakban
is felírható:
Az  esetben a
esetben a 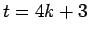 -ra már nem kapunk pontos értéket a két DIXMIER-tétel alapján.
Az
-ra már nem kapunk pontos értéket a két DIXMIER-tétel alapján.
Az  további növelésével egyre ritkábban fordul elő, hogy a két tétel
oszthatósági feltételei teljesülnek, így ezen az úton további általánosabb eredmények nem
nyerhetők. Azt, hogy mégsem érdektelen a két tétel későbbi használata,
például a
további növelésével egyre ritkábban fordul elő, hogy a két tétel
oszthatósági feltételei teljesülnek, így ezen az úton további általánosabb eredmények nem
nyerhetők. Azt, hogy mégsem érdektelen a két tétel későbbi használata,
például a  eset pontos számolásával is indokolhatjuk.
eset pontos számolásával is indokolhatjuk.
Más úton V. LEVnek [19] sikerült kiterjesztenie az
ERDŐS-GRA-HAM-tétel érvényességi körét. Belátta, hogy a
 -ra vonatkozó formula
egészen
-ra vonatkozó formula
egészen  -ig teljesül az eredetileg megfogalmazott formában.
Bizonyításában FREIMAN két erős tételére támaszkodik.
Itt lényeges, hogy ,,majdnem sűrű'' halmazok szerepeljenek, tehát ezen az
úton sem nyerhetünk új formulákat. Az előbb említett 3.2.7. DIXMIER-tétellel azonban
pontosan meghatározzuk
-ig teljesül az eredetileg megfogalmazott formában.
Bizonyításában FREIMAN két erős tételére támaszkodik.
Itt lényeges, hogy ,,majdnem sűrű'' halmazok szerepeljenek, tehát ezen az
úton sem nyerhetünk új formulákat. Az előbb említett 3.2.7. DIXMIER-tétellel azonban
pontosan meghatározzuk
 -et:
-et:
Itt elfogynak a szakirodalomban az általánosan igaz formulák.
Ez természetesen nem jelenti azt, hogy nem tudunk meghatározni bizonyos
feltételek teljesülése esetén további  -ket, pl.
-ket, pl.  , ha
, ha
 , illetve
, illetve


 is azonnal adódik a DIXMIER-tételekből.
is azonnal adódik a DIXMIER-tételekből.




Next: A meghatározása
Up: Az extremális Frobenius-probléma
Previous: Néhány becslés -ra
Tartalomjegyzék
root
2004-12-04
![]() -vel kapcsolatban több fontos
részeredmény is ismert.
-vel kapcsolatban több fontos
részeredmény is ismert.



![]() -re.
-re.



![]() Ekkor két esetet vizsgálunk aszerint, hogy
a
Ekkor két esetet vizsgálunk aszerint, hogy
a ![]() páros vagy páratlan. A páros esetben a 3.2.7. Tétel alapján
páros vagy páratlan. A páros esetben a 3.2.7. Tétel alapján


![]() esetben is.
Legyen először
esetben is.
Legyen először ![]() , vagy
, vagy ![]() . Alkalmazhatjuk a 3.2.7. Tételt,
és kapjuk, hogy
. Alkalmazhatjuk a 3.2.7. Tételt,
és kapjuk, hogy



![]() esetben a
esetben a ![]() -ra már nem kapunk pontos értéket a két DIXMIER-tétel alapján.
Az
-ra már nem kapunk pontos értéket a két DIXMIER-tétel alapján.
Az ![]() további növelésével egyre ritkábban fordul elő, hogy a két tétel
oszthatósági feltételei teljesülnek, így ezen az úton további általánosabb eredmények nem
nyerhetők. Azt, hogy mégsem érdektelen a két tétel későbbi használata,
például a
további növelésével egyre ritkábban fordul elő, hogy a két tétel
oszthatósági feltételei teljesülnek, így ezen az úton további általánosabb eredmények nem
nyerhetők. Azt, hogy mégsem érdektelen a két tétel későbbi használata,
például a ![]() eset pontos számolásával is indokolhatjuk.
eset pontos számolásával is indokolhatjuk.
![]() -ra vonatkozó formula
egészen
-ra vonatkozó formula
egészen ![]() -ig teljesül az eredetileg megfogalmazott formában.
Bizonyításában FREIMAN két erős tételére támaszkodik.
Itt lényeges, hogy ,,majdnem sűrű'' halmazok szerepeljenek, tehát ezen az
úton sem nyerhetünk új formulákat. Az előbb említett 3.2.7. DIXMIER-tétellel azonban
pontosan meghatározzuk
-ig teljesül az eredetileg megfogalmazott formában.
Bizonyításában FREIMAN két erős tételére támaszkodik.
Itt lényeges, hogy ,,majdnem sűrű'' halmazok szerepeljenek, tehát ezen az
úton sem nyerhetünk új formulákat. Az előbb említett 3.2.7. DIXMIER-tétellel azonban
pontosan meghatározzuk
![]() -et:
-et:
