



Next: Az ERDŐS-GRAHAM-sejtés
Up: A nem felírható számok
Previous: A nem felírható számok
Tartalomjegyzék
Már SYLVESTER 1884-ben vizsgálta és meg is oldotta azt a kérdést, hogy
két különböző ,,érme'' esetén hány olyan pozitív egész szám van, amely nem írható
fel e két szám lineáris kombinációjaként. Ezt az eredményt a 2. fejezet
8. feladatában mutattuk be.
Elsősorban SELMER norvég matematikus munkássága révén gyakorlatilag mindegyik
olyan esetben kiszámítható
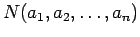 , amikor
már előbb
, amikor
már előbb
 -et ismerjük.
A kiszámításhoz egy áttekint-hető modellt használt. A
-et ismerjük.
A kiszámításhoz egy áttekint-hető modellt használt. A
 maradékosztályok
mindegyikéből megkereste a legkisebb felírható számot és így össze tudta számolni
a nem felírhatókat.
maradékosztályok
mindegyikéből megkereste a legkisebb felírható számot és így össze tudta számolni
a nem felírhatókat.
Legyen 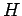 egy teljes maradékrendszer mod
egy teljes maradékrendszer mod 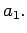 Minden
Minden
 -hoz van olyan
-hoz van olyan
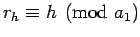 , amely felírható
, amely felírható
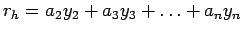 alakban és a legkisebb.
Ezekkel a jelölésekkel
alakban és a legkisebb.
Ezekkel a jelölésekkel
A módszer gyakorlati alkalmazásaira a 2. fejezetben több példát is mutattunk.
A 9. feladatban középiskolai eszközökkel kiszámítottuk
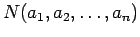 -et, amikor az
-et, amikor az  -k számtani sorozatot
alkotnak.
Speciálisan, amikor
-k számtani sorozatot
alkotnak.
Speciálisan, amikor  , akkor szomszédos számok esetében kapjuk a nem felírhatók
számát (ld. 15. feladat). Erre jelen fejezet második részében még
visszatérünk. SELMER [28] a sorozatokra vonatkozó
formulát továbbfejlesztette ,,majdnem'' számtani sorozatokra is.
, akkor szomszédos számok esetében kapjuk a nem felírhatók
számát (ld. 15. feladat). Erre jelen fejezet második részében még
visszatérünk. SELMER [28] a sorozatokra vonatkozó
formulát továbbfejlesztette ,,majdnem'' számtani sorozatokra is.
TÉTEL 4.1.3
Legyenek
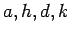 pozitív egészek és
pozitív egészek és  Ekkor
ahol
Ekkor
ahol
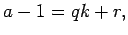

Végül TINAGLIA [31]  -ra vonatkozó, a szokványostól nagyon eltérő
megfogalmazású eredményét ismertetjük.
-ra vonatkozó, a szokványostól nagyon eltérő
megfogalmazású eredményét ismertetjük.
TÉTEL 4.1.4
Legyenek  és
és  a legkisebb olyan pozitív egész számok,
amelyek kielégítik az
diofantoszi egyenleteket úgy, hogy
a legkisebb olyan pozitív egész számok,
amelyek kielégítik az
diofantoszi egyenleteket úgy, hogy
 Ezekkel a jelölésekkel
Ezekkel a jelölésekkel
Az előbbi feltételekkel felírt  számokat JOHNSON-egészeknek
nevezik.
számokat JOHNSON-egészeknek
nevezik.
Becslések természetesen
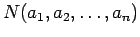 -nel kapcsolatban is
ismertek. A legegyszerűbb talán NIJENHUIS és WILF
eredménye [22]. A 0-tól a
-nel kapcsolatban is
ismertek. A legegyszerűbb talán NIJENHUIS és WILF
eredménye [22]. A 0-tól a
 -ig pontosan
-ig pontosan
 darab nemnegatív szám van. Ezeket párba állíthatjuk
úgy, hogy az egyes párok összege minden esetben
darab nemnegatív szám van. Ezeket párba állíthatjuk
úgy, hogy az egyes párok összege minden esetben
 legyen:
legyen:
Mivel
 nem írható fel az
nem írható fel az  -k segítségével,
ezért a párokban szereplő számok közül legalább az egyik szintén ilyen lesz,
így kaptuk, hogy
-k segítségével,
ezért a párokban szereplő számok közül legalább az egyik szintén ilyen lesz,
így kaptuk, hogy
Amennyiben
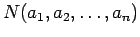 -et olyan esetekben is meg
tudnánk ha-tározni, amelyekben
-et olyan esetekben is meg
tudnánk ha-tározni, amelyekben
 -et nem
ismerjük, jó felső becslést kaphatnánk a legnagyobb nem felírható
számra, és fordítva. Máris érthető, hogy a témakörnek ez a szelete is rohamosan fejlődik.
A párhuzamok lehetősége miatt megemlítünk még egy alsó becslést, amely
KILLINGBERGTROtól [15] származik:
-et nem
ismerjük, jó felső becslést kaphatnánk a legnagyobb nem felírható
számra, és fordítva. Máris érthető, hogy a témakörnek ez a szelete is rohamosan fejlődik.
A párhuzamok lehetősége miatt megemlítünk még egy alsó becslést, amely
KILLINGBERGTROtól [15] származik:
Összevetve a 3.1.6. és 3.1.7. Tételekkel, ahol
 -re ismertettünk alsó becsléseket, látjuk, hogy
ezekben a becslésekben a két függvény,
-re ismertettünk alsó becsléseket, látjuk, hogy
ezekben a becslésekben a két függvény,  és
és  gyakorlatilag megegyezik.
Olyan konstrukció tetsző-leges
gyakorlatilag megegyezik.
Olyan konstrukció tetsző-leges  -re adható, ahol ez az egyenlőség
ténylegesen be is következik.
-re adható, ahol ez az egyenlőség
ténylegesen be is következik.




Next: Az ERDŐS-GRAHAM-sejtés
Up: A nem felírható számok
Previous: A nem felírható számok
Tartalomjegyzék
root
2004-12-04


![]() egy teljes maradékrendszer mod
egy teljes maradékrendszer mod ![]() Minden
Minden
![]() -hoz van olyan
-hoz van olyan
![]() , amely felírható
, amely felírható
![]() alakban és a legkisebb.
Ezekkel a jelölésekkel
alakban és a legkisebb.
Ezekkel a jelölésekkel


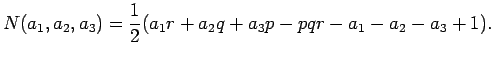
![]() számokat JOHNSON-egészeknek
nevezik.
számokat JOHNSON-egészeknek
nevezik.
![]() -nel kapcsolatban is
ismertek. A legegyszerűbb talán NIJENHUIS és WILF
eredménye [22]. A 0-tól a
-nel kapcsolatban is
ismertek. A legegyszerűbb talán NIJENHUIS és WILF
eredménye [22]. A 0-tól a
![]() -ig pontosan
-ig pontosan
![]() darab nemnegatív szám van. Ezeket párba állíthatjuk
úgy, hogy az egyes párok összege minden esetben
darab nemnegatív szám van. Ezeket párba állíthatjuk
úgy, hogy az egyes párok összege minden esetben
![]() legyen:
legyen:
![]() nem írható fel az
nem írható fel az ![]() -k segítségével,
ezért a párokban szereplő számok közül legalább az egyik szintén ilyen lesz,
így kaptuk, hogy
-k segítségével,
ezért a párokban szereplő számok közül legalább az egyik szintén ilyen lesz,
így kaptuk, hogy

