Ízelítő az extremális Frobenius-problémából

Az előzőekben láttuk, hogy $G(a_1, a_2, \ldots ,a_n)$ meghatározása sok esetben szinte megoldhatatlan feladatnak mutatkozik. Talán éppen ez az oka, hogy számos, elsősorban felső becslés ismert, amelyek a legkülönfélébb specializáló feltételek mellett adnak korlátot a legnagyobb nem felírható számra. Az egyik első ilyen becslést ERDŐS és GRAHAM [6] adták 1972-ben a Kneser-tételt felhasználva:

$$G(a_1, a_2, \ldots , a_n) \le 2a_{n-1} \left\lfloor \frac {a_n}{n}\right\rfloor-a_n.$$

Valószínűleg a becslések adták az ötletet annak a vizsgálatához, hogy adott korlátig választva rögzített darabszámú $a_i$-t, mely esetben lesz maximális a nem felírható legnagyobb szám. Erre vonatkozik a $g(n, t)$ jelölés:

$$g(n, t)= \max$$    $$G(a_1, a_2, \ldots , a_n),$$

ahol mindegyik $a_i$ legfeljebb $t$ és legnagyobb közös osztójuk $1$. Az egy-szerűbb kezelhetőség miatt az $\{a_1, a_2, \ldots , a_n \}$ halmazt a továbbiakban sokszor $A$-val, az $A$ elemeivel felírható természetes számok halmazát $S(A)$-val jelöljük.

Ezt követően a sok további értékes becslés közül DIXMIER [4, Thm.3] tételét szeretném kiemelni, amely ugyancsak felhasználja a Kneser-tételt.

$$g(n, t) \le (v-1)(t-r-1)-1, t-1=v(n-1)-r 0 \le r < n-1.$$ (2.3.1)

Most néhány speciális esetben határozzuk meg $g(n, t)$-t. Az alábbi feladat megoldása azonnal adódik a 3. feladatból.

FELADAT 11   Legyen $t>2$ pozitív egész szám. Ekkor

$$g(2, t)=(t-1)(t-2)-1.$$

DIXMIER előbbi tételének alkalmazásával megoldhatók az $n=3$ és $n=4$ esetek is. A $g(3, t)$ értékét LEWIN [20] már 20 évvel korábban kiszámította:

$$g(3, t)=\left\lfloor\frac{1}{2}(t-2)^2\right\rfloor-1.$$

A ,,túl sok" érme irányából sűrűségi megfontolásokkal közelítette meg a problémát NAGATA és MATSUMURA [21]. Tételük a $k$-ra vonatkozó teljes indukcióval is bizonyítható.

FELADAT 12   Legyenek $n$ és $k$ pozitív egészek, $k \le n-1.$ Ekkor

$$g(n, n+k)= 2k-1.$$

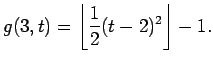
Ezt az eredményt fejlesztette tovább ERDŐS [5] egy kitűzött feladatában:

FELADAT 13   Ha $n > 2$, akkor

$$g(n, 2n)=2n+1, \indent g(n,2n+1)=\left\{ \begin{gathered}2n+5, \... ...{3};\\ 2n+3, \text{ ha } n \equiv 2 \pmod{3}. \end{gathered} \text{ } \right.$$

Az első, kevésbé összetett állítás igazolása a nehezebb tételek bizonyítási módszereibe is betekintést enged. Először azt látjuk be, hogy minden lehetséges $A$ halmazra

$$G(A) \le 2n+1.$$

Legyen $a_n=2n,$ hiszen ellenkező esetben a 12. feladat alapján

$$G(A) \le 2(n-1)-1=2n-3.$$

Ha a $2n+1$ két $A$-beli összege, akkor hozzávehetjük az $A$-hoz.

$$G(A')=G(A \cup \{2n+1\}) \le 2(n+1)-3=2n-1.$$

A továbbiakban feltehetjük, hogy $2n+1\not=a_i+a_j.$

Eszerint $L$ és $2n+1-L$ közül legfeljebb az egyik van $A$-ban, de az elemek száma éppen $n$, így pontosan az egyik van $A$-ban.

Tegyük fel először, hogy $a_{n-1}=2n-1$. Ekkor az előbbiek miatt $2 \not\in A.$ Legyen $r>2$ a legkisebb $A$-beli elem. Így

$$2n, 2n-1, \ldots , 2n+1-(r-1)=2n-r+2 \in A.$$

Ezekhez az $r$-et hozzáadva,

$$2n-r+2+r=2n+2 \in S(A)$$    és $$2n+1-(r-2)+r=2n+3 \in S(A).$$

Hozzávéve ezt a két számot $A$-hoz kapunk egy $n+2$ elemű $A'$ halmazt, amelyre

$$G(A') \le g(n+2, n+2+n+1)=2(n+1)-1=2n+1.$$

Feltehetjük tehát ezután, hogy $a_{n-1}<2n-1$, azaz $2 \in A$ és így minden páros szám $S(A)$-ban van. A legkisebb páratlan $A$-beli számhoz (ilyen biztosan van, hiszen az elemek relatív prímek) hozzádva a $2$-t minden ennél az elemnél nagyobb páratlan számhoz is eljuthatunk. Ezzel igazoltuk, hogy minden lehetséges $A$ halmazra

$$G(A) \le 2n+1,$$    azaz $$g(n, 2n) \le 2n+1.$$

Meg kell még mutatni, hogy van olyan $A$, amelyre az egyenlőség teljesül. Legyen $A=\{n+1, n+2, \ldots , 2n\}.$ Látható, hogy $2(n+1)$ és minden ennél nagyobb szám $S(A)$-ban van, így

$$G(A)=2n+1.$$    $$\blacksquare$$

A fenti gondolatmenet jelentős kiterjesztésével ERDŐS és GRAHAM [6] igazolták, hogy rögzített $k$-ra, ha az $n$ elegendően nagy
$(n \ge 9k^2+15k+2),$ akkor

$$g(n, 2n+k)= \left\{ \begin{gathered}2n+4k+1,\text{ } \text{ ha } ... ...1, \text{ }\text{ ha } n-k \equiv 1 \pmod{3}. \end{gathered} \right.\tag{2.3.2}$$

Bizonyításuk összetett, de az egyszerűbb rész egy-egy olyan $A$ kons-trukciója, amellyel az egyenlőség teljesül.

FELADAT 14   Legyenek $n$ és $k$ pozitív egészek $(n \ge 9k^2+15k+2).$ Adjunk meg olyan $n$ elemű $A$ halmazt, amelyre teljesül, hogy elemei legnagyobb közös osztója $1$, mindannyian kisebbek, mint $2n+k+1$ és

$$G(A)= \left\{ \begin{gathered}2n+4k+1, \text{ ha } n-k \not \equi... ...pmod{3};\\ 2n+4k-1, \text{ ha } n-k \equiv 1 \pmod{3}. \end{gathered} \right.$$

Legyen elsőként $n-k \equiv 1 \pmod {3}.$ Írjuk az $n$-et $n=3m+k+1$ alakban és legyen $A$ a következő:

$$A=\bigcup\limits_{i=1}^{2m+k} \{3i\}\cup \bigcup \limits_{j=1}^{m+1}\{6m+3k+5-3j\}.$$

$S(A)$ legkisebb eleme, amely $1$-gyel kongruens modulo $3$:

$$2(3m+3k+2)=6m+6k+4.$$

Ennek megfelelően

$$6m+6k+1=2n+4k-1 \not \in S(A).$$

Legyen most $n-k \equiv 2 \pmod {3}.$ Írjuk az $n$-et $n=3m+k+2$ alakban és legyen az $A$ halmaz:

$$A=\bigcup\limits_{i=1}^{2m+k+1} \{3i\}\cup \bigcup \limits_{j=1}^{m+1}\{6m+3k+7-3j\}.$$

Az $S(A)$ legkisebb eleme, amely $2$-vel kongruens modulo $3$ a

$$2(3m+3k+4)=6m+6k+8=2n+4k+4.$$

A harmadik esetben ugyanilyen elven tudunk megadni megfelelő hal-mazt.  $\blacksquare$

$g(n, t)$ meghatározása szintén igen sok esetben megoldatlan prob-léma. LEV [19] megmutatta, hogy ERDŐS és GRAHAM (2.3.2) eredménye kiterjeszthető $t \le 3n-2$-ig. E dolgozat szerzője [17]-ben igazolta, hogy a (2.3.1)-ben megadott becslés a DIXMIER által nem említett további esetekben is pontos. Nevezetesen, ha $2 \le d < n, \newline 0 \le k \le n-d,$ akkor $n-k \equiv 0$    vagy$-1 \pmod {d+1}$ esetén

$$g(n, dn+k)=d(d-1)n+2dk+d^2-d-1.\tag{2.3.3}$$

A legnagyobb nem felírható számot adó konstrukciók itt is ,,két elem által'' generáltak.

Az extremális Frobenius-probléma egy másik kérdése: hogyan kell választanunk $n$ darab különböző címletet $t$-ig, hogy a nem felírható számok száma maximális legyen. ERDŐS és GRAHAM azt sejtette, hogy akkor lesz a legtöbb a nem felírható szám, amikor az elemeket szomszédosaknak választjuk [7, 86. oldal]. A sejtés DIXMIER egyik tételének [4, Thm.2] felhasználásával igazolható. További kisebb számolással az is kideríthető, hogy a (2.3.3) bizonyításához megadott halmazok esetében, bár a legnagyobb nem felírható szám jóval nagyobb, a nem felírhatók száma a 15. feladatban szereplő szomszédosakkal mégis megegyező [17]. Számoljuk ki, hogy mennyi ebben az esetben ez a szám! (Ez tulajdonképpen a 9. feladat speciális esete, az alábbi képlet az ottaniból is levezethető, de itt egyszerűbben is eljárhatunk, és ezt mutatjuk be most.)

FELADAT 15   Legyenek $n$ és $t$ egészek, $1 < n \le t,$ továbbá
$t=q(n-1)+r,$ ahol $1 \le r \le n-1.$ Ekkor

$$N(t-n+1,t-n+2, \dots , t)=\frac {(t-n+r-1)q} {2}.$$

Mivel $a_i=t-n+i$ szomszédos egész számok, ezért a

$$J_m=[m(t-n+1), mt]$$

intervallumban található egészek mind előállíthatók, ha $m=1, 2, \dots.$ A nem felírható számok a $J_1$ intervallum előtt, a $J_1$ és $J_2$ között, ..., $J_{m-1}$ és $J_m$ között helyezkednek el, amíg ezek az intervallumok diszjunktak, azaz $(m-1)t<m(t-n+1),$ vagy, ami ezzel ekvivalens $m(n-1) < t.$ Az utolsó ilyen érték az $m=q.$ Így azoknak a számoknak a száma, amelyek nem írhatók fel:

$$\sum _{m=1}^q [m(t-n+1)-(m-1)t-1]=\sum _{m=1}^q (t-mn+m-1)=$$

$$=qt-\frac {q(q+1)} {2}(n-1)-q=\frac {q}{2}[2t-(q+1)(n-1)-2]=$$

$$=\frac{q}{2}[t+q(n-1)+r-(q+1)(n-1)-2]=\frac {(t-n+r-1)q}{2}.$$     $$\blacksquare$$

A fenti összeállításban szereplő feladatok mindegyike megfelelő elő-készítés után a középiskolai tanítás során is tárgyalható.

SYLVESTER 1884-ben megjelent, kiindulásnak tekinthető első közlésétől [30], ahol egyszerű eszközökkel tárgyalja a kétismeretlenes esetet, egy teljes évszázadnak kellett eltelnie ahhoz, hogy a problémakör előforduljon a versenyeken (1. és 2. feladat), majd hamarosan egy iskolai feladatgyűjteményben (Bergengóc példatár: 152. és 158. feladat)[8], és így reményeink szerint a későbbiekben rendszeresen a matematika iránt érdeklődő tanulóknál a különféle foglalkozásokon is.